Understanding Focal Length and Field of View
Authors: Gregory Hollows, Nicholas James
This is Section 1.3 of the Imaging Resource Guide.
Focal Length
The focal length of a lens is a fundamental parameter that describes how strongly it focuses or diverges light. A large focal length indicates that light is bent gradually while a short focal length indicates that the light is bent at sharp angles. In general, lenses with positive focal lengths converge light while lenses with negative focal lengths cause light to diverge, although there are some exceptions based on the distance from the lens to the object being imaged.
Field of View
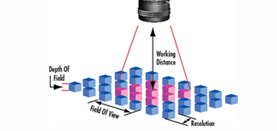
Field of view describes the viewable area that can be imaged by a lens system. This is the portion of the object that fills the camera’s sensor. This can be described by the physical area which can be imaged, such as a horizontal or vertical field of view in mm, or an angular field of view specified in degrees. The relationships between focal length and field of view are shown below.
Fixed Focal Length Lenses
A fixed focal length lens, also known as a conventional or entocentric lens, is a lens with a fixed angular field of view (AFOV). By focusing the lens for different working distances (WDs), differently sized field of view (FOV) can be obtained, though the viewing angle is constant. AFOV is typically specified as the full angle (in degrees) associated with the horizontal dimension (width) of the sensor that the lens is to be used with.
Note: Fixed focal length lenses should not be confused with fixed focus lenses. Fixed focal length lenses can be focused for different distances; fixed focus lenses are intended for use at a single, specific WD. Examples of fixed focus lenses are many telecentric lenses and microscope objectives.
The focal length of a lens defines the AFOV. For a given sensor size, the shorter the focal length, the wider the AFOV. Additionally, the shorter the focal length of the lens, the shorter the distance needed to obtain the same FOV compared to a longer focal length lens. For a simple, thin convex lens, the focal length is the distance from the back surface of the lens to the plane of the image formed of an object placed infinitely far in front of the lens. From this definition, it can be shown that the AFOV of a lens is related to the focal length (Equation 1), where $ \small{f} $ is the focal length and $ \small{H} $ is the sensor size (Figure 1).

Figure 1: For a given sensor size, H, shorter focal lengths produce wider AFOV’s.
In general, however, the focal length is measured from the rear principal plane, rarely located at the mechanical back of an imaging lens; this is one of the reasons why WDs calculated using paraxial equations are only approximations and the mechanical design of a system should only be laid out using data produced by computer simulation or data taken from lens specification tables. Paraxial calculations, as from lens calculators, are a good starting point to speed the lens selection process, but the numerical values produced should be used with caution.
When using fixed focal length lenses, there are three ways to change the FOV of the system (camera and lens). The first and often easiest option is to change the WD from the lens to the object; moving the lens farther away from the object plane increases the FOV. The second option is to swap out the lens with one of a different focal length. The third option is to change the size of the sensor; a larger sensor will yield a larger FOV for the same WD, as defined in Equation 1.
While it may be convenient to have a very wide AFOV, there are some negatives to consider. First, the level of distortion that is associated with some short focal length lenses can greatly influence the actual AFOV and can cause variations in the angle with respect to WD due to distortion. Next, short focal length lenses generally struggle to obtain the highest level of performance when compared against longer focal length options (see Best Practice #3 in Best Practices for Better Imaging). Additionally, short focal length lenses can have difficulties covering medium to large sensor sizes, which can limit their usability, as discussed in Relative Illumination, Roll-Off, and Vignetting.
Another way to change the FOV of a system is to use either a varifocal lens or a zoom lens; these types of lenses allow for adjustment of their focal lengths and thus have variable AFOV. Varifocal and zoom lenses often have size and cost drawbacks compared to fixed focal length lenses, and often cannot offer the same level of performance as fixed focal length lenses.
Using WD and FOV to Determine Focal Length
In many applications, the required distance from an object and the desired FOV (typically the size of the object with additional buffer space) are known quantities. This information can be used to directly determine the required AFOV via Equation 2. Equation 2 is the equivalent of finding the vertex angle of a triangle with its height equal to the WD and its base equal to the horizontal FOV, or HFOV, as shown in Figure 2. Note: In practice, the vertex of this triangle is rarely located at the mechanical front of the lens, from which WD is measured, and is only to be used as an approximation unless the entrance pupil location is known.
Once the required AFOV has been determined, the focal length can be approximated using Equation 1 and the proper lens can be chosen from a lens specification table or datasheet by finding the closest available focal length with the necessary AFOV for the sensor being used.
The 14.25° derived in Example 1 (see white box below) can be used to determine the lens that is needed, but the sensor size must also be chosen. As the sensor size is increased or decreased it will change how much of the lens’s image is utilized; this will alter the AFOV of the system and thus the overall FOV. The larger the sensor, the larger the obtainable AFOV for the same focal length. For example, a 25mm lens could be used with a ½” (6.4mm horizontal) sensor or a 35mm lens could be used with a 2/3” (8.8mm horizontal) sensor as they would both approximately produce a 14.5° AFOV on their respective sensors. Alternatively, if the sensor has already been chosen, the focal length can be determined directly from the FOV and WD by substituting Equation 1 in Equation 2, as shown in Equation 3.
(3)$$ f = \frac{ \left( H \times \text{WD} \right) }{\text{FOV}} $$
As previously stated, some amount of flexibility to the system’s WD should be factored in, as the above examples are only first-order approximations and they also do not take distortion into account.

Figure 2: Relationship between FOV, sensor size, and WD for a given AFOV.
Calculating FOV Using a Lens with a Fixed Magnification
Generally, lenses that have fixed magnifications have fixed or limited WD ranges. While using a telecentric or other fixed magnification lens can be more constraining, as they do not allow for different FOVs by varying the WD, the calculations for them are very direct, as shown in Equation 4.
(4)$$ \text{FOV} = \frac{ H }{m} $$
Since the desired FOV and sensor are often known, the lens selection process can be simplified by using Equation 5.
(5)$$ m = \frac{ H }{\text{FOV}} $$
If the required magnification is already known and the WD is constrained, Equation 3 can be rearranged (replacing $ \small{ \tfrac{H}{\text{FOV}}} $ with magnification) and used to determine an appropriate fixed focal length lens, as shown in Equation 6.
(6)$$ m = \frac{ f }{\text{WD}} $$
Be aware that Equation 6 is an approximation and will rapidly deteriorate for magnifications greater than 0.1 or for short WDs. For magnifications beyond 0.1, either a fixed magnification lens or computer simulations (e.g. Zemax) with the appropriate lens model should be used. For the same reasons, lens calculators commonly found on the internet should only be used for reference. When in doubt, consult a lens specification table.
Note: Horizontal FOV is typically used in discussions of FOV as a matter of convenience, but the sensor aspect ratio (ratio of a sensor’s width to its height) must be taken into account to ensure that the entire object fits into the image where the aspect ratio is used as a fraction (e.g. 4:3 = 4/3), Equation 7.
(7)$$ \text{Horizontal FOV} = \text{Vertical FOV} \times \text{Aspect Ratio} $$
While most sensors are 4:3, 5:4 and 1:1 are also quite common. This distinction in aspect ratio also leads to varying dimensions of sensors of the same sensor format. All of the equations used in this section can also be used for vertical FOV as long as the sensor’s vertical dimension is substituted in for the horizontal dimension specified in the equations.
LENS FOCAL LENGTH EXAMPLES
Using WD and FOV to Determine Focal Length
Example 1: For a system with a desired WD of 200mm and a FOV of 50mm, what is the AFOV?
\begin{align}\text{AFOV} & = 2 \times \tan^{-1} \left( {\frac{50 \text{mm}}{2 \times 200 \text{mm}}} \right) \\ \text{AFOV} & = 14.25° \end{align}
Calculating FOV Using a Lens with a Fixed Magnification
Example 2: For an application using a ½” sensor, which has a horizontal sensor size of 6.4mm, a horizontal FOV of 25mm is desired.
\begin{align} m & = \frac{6.4 \text{mm}}{25 \text{mm}} \\ m & = 0.256 \text{X} \\ \end{align}
By reviewing a list of fixed magnification or telecentric lenses, a proper magnification can be selected.
Note: As the magnification increases, the size of the FOV will decrease; a magnification that is lower than what is calculated is usually desirable so that the full FOV can be visualized. In the case of Example 2, a 0.25X lens is the closest common option, which yields a 25.6mm FOV on the same sensor.













 Previous Section
Previous Section 




























































































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act