
Source to Lens 1 Distance (mm): --
Lens 1 to Lens 2 Distance (mm): --
Lens 2 to Spot Diameter Distance (mm): --
System Length (mm): --
Spot Diameter (mm): --
Input Numerical Aperture, NA: --
Output Numerical Aperture, NA: --
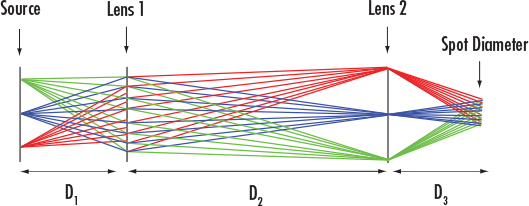
| d1 | Source to Lens 1 Distance |
| d2 | Lens 1 to Lens 2 Distance |
| d3 | Lens 2 to Spot Distance |
| DL1 | Diameter of Lens 1 |
| DL2 | Diameter of Lens 2 |
| FL1 | Focal Length of Lens 1 |
| FL2 | Focal Length of Lens 2 |
| Dsource | Source Diameter |
| Dspot | Spot Diameter |
| NAinput | Input Numerical Aperture |
| NAoutput | Output Numerical Aperture |
Mathematically determine how to configure a source and two lenses into a Koehler Illumination setup. Calculator uses the paraxial lens approximation and enables an initial lens selection. Once lenses are selected, Edmund Optics recommends modeling one's Koehler Illumination setup in optical design software such as Zemax, CodeV, or FRED to analyze and revise as needed. Please note that performance will vary based on source and lens selections.
or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act